時系列予測

Quiverで時系列予測変換を使って予測を作成できます。予測とは、解析の既存の時系列プロットを将来に向けて投影するものです。Quiverの予測は視覚的でインタラクティブに構築されます。予測の結果は、予測されたデータを表す時系列プロットであり、この時系列プロットは、Quiverの時系列変換を使用してさらに変換できます。

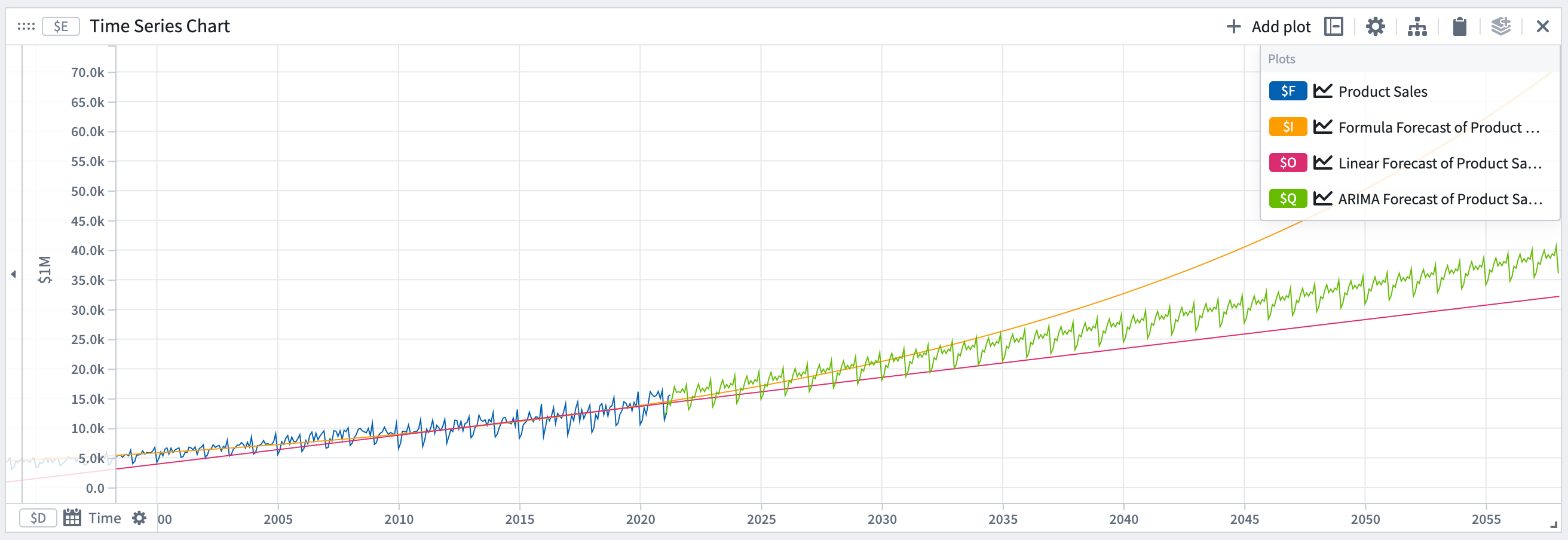
予測を作成する

このセクションを説明するために、線形予測を例に使用します。以下のセクションでは、各種類の予測について詳しく説明しています。

1. 予測したい時系列をQuiver解析に追加します。解析の上部にあるバーから時系列をクリックして検索バーを開きます。この例では、製品の販売予測を行いたいとします。

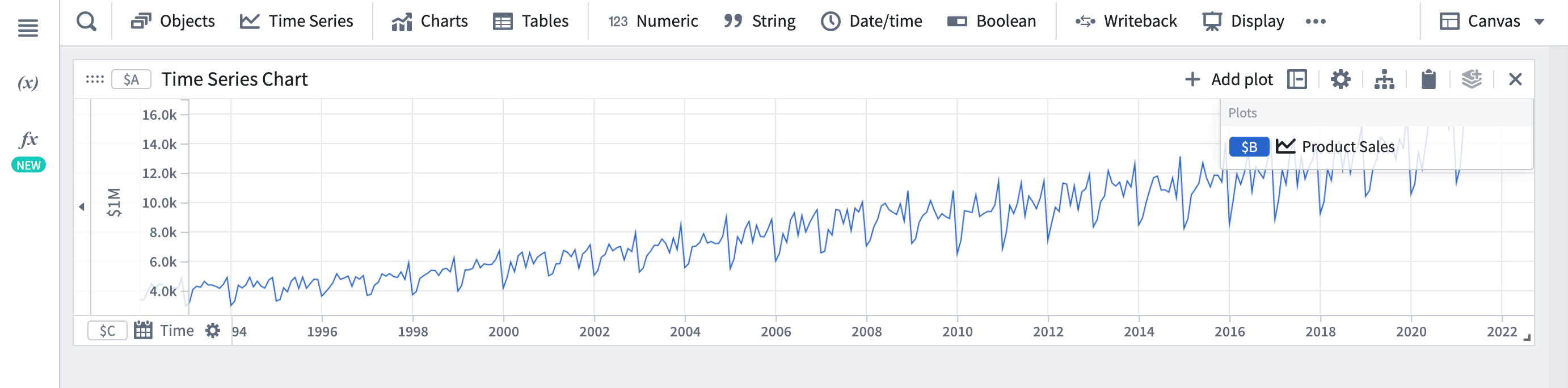
2. 時系列メニューから時系列予測を選択します。

3. 予測エディタで線形予測タイプを選択し、ステップ1で追加したプロットを入力プロットとして選択します。

これにより、デフォルトで入力プロットの全範囲にフィットする時系列プロット（この場合は線）が生成されます。時軸は、入力時系列プロットのままです。将来の予測をさらに見るには、x軸でズームアウトできます。

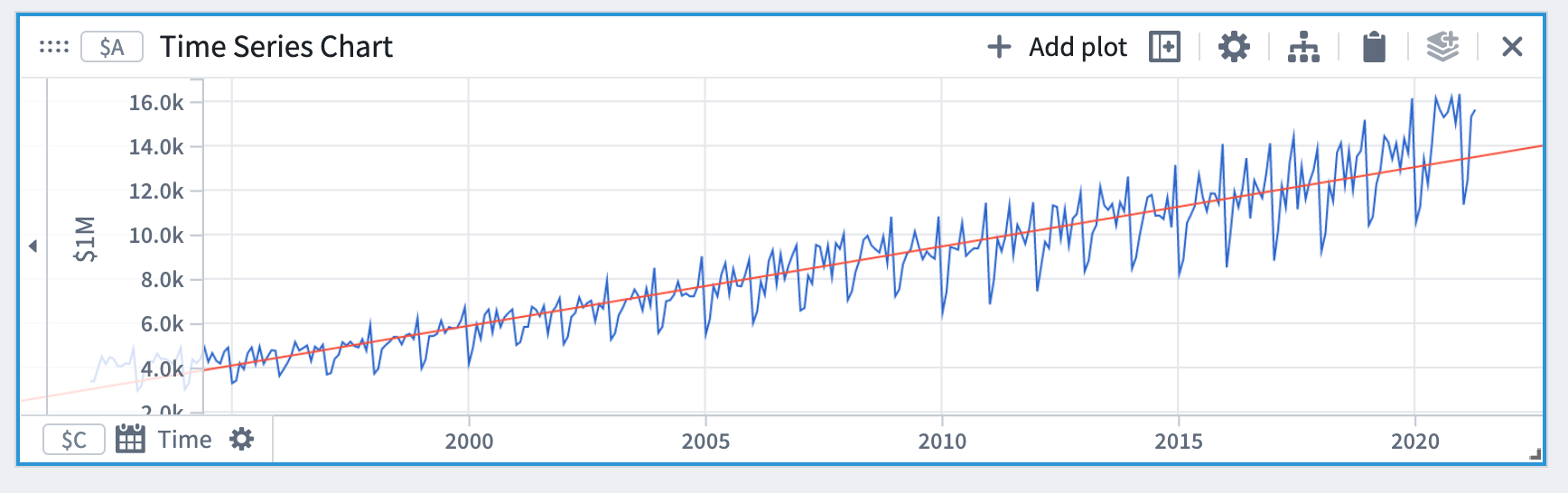
予測エディタの予測詳細セクションで、係数の値を確認できます。

線形予測の例では、係数は m（傾き）と c（オフセット）です。

任意のステップ

1. フィッティングを特定の時間範囲に制限するには、Use Training Time Rangeのトグルをオンにし、時間範囲のパラメーターを選択します。

ここでは、トレーニングの時間範囲を全履歴ではなく2015年から2020年に設定しています。その結果、予測のパラメータ（傾きとオフセット）が変更され、トレーニングの時間範囲で予測がより正確になります。特定の時間が未来の振る舞いを示すと考える場合に便利です。

2. 係数の境界を設定します。エディタの係数セクションで、境界を設定したい係数のトグルをオンにします。この例では、この予測の傾き係数の境界を設定すると、両方の係数が変更されます。

3. 損失の定義を選択します。デフォルトの損失は二乗差の合計で、他のオプションは最大絶対差と絶対差の合計です。予測をトレーニングデータにフィットさせる際に、損失を最小化するようにパラメータが選択されます。損失の種類によって、異なる予測が得られます。詳細は損失セクションを参照してください。

この例では、損失の定義を変更すると、予測の係数が異なります。

さまざまな種類の予測

このセクションでは、さまざまな種類の予測とその設定オプションについて詳しく説明します。このドキュメントの残りの部分では、予測される量を y または y(t)（時刻 t での y）として参照します。

定数

定数予測は、量 y が一定になると仮定します。

数学的な形式: y = a

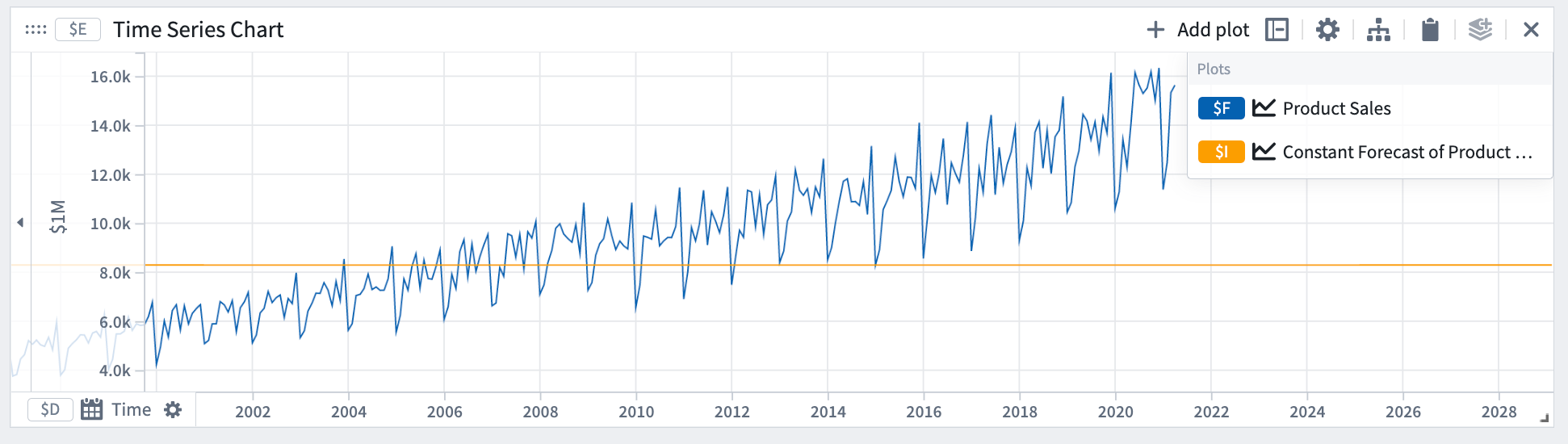
この例では、定数予測はデータの傾きや周期性を捉えていないことがわかります。

線形

線形予測は、量 y が線形の傾向に従うと仮定します。

数学的な形式: y = a*t + b

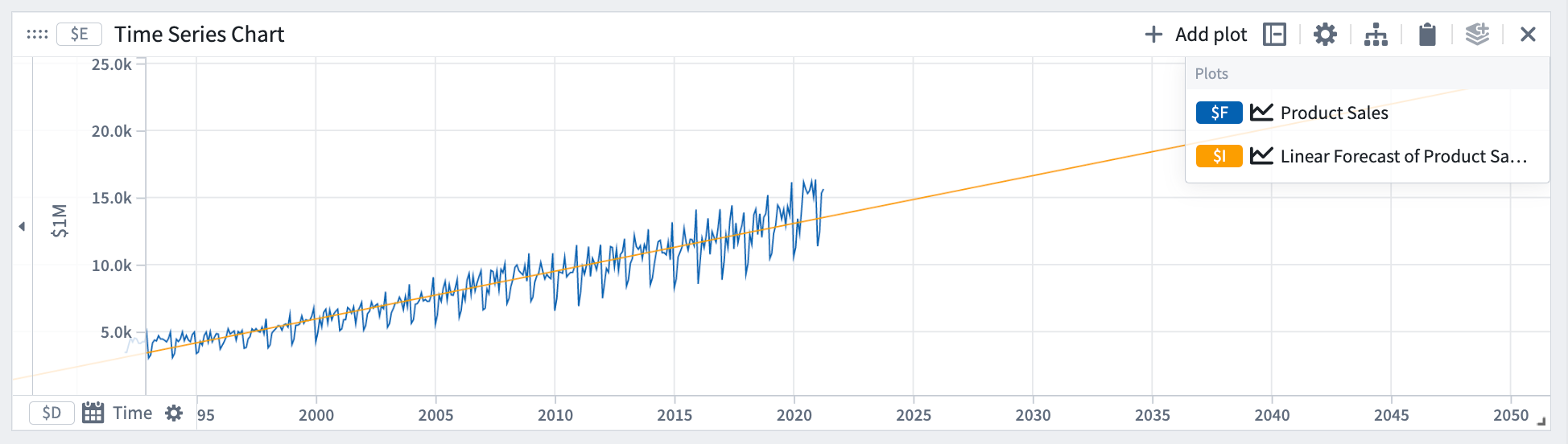
この例では、線形予測は傾きを捉えていますが、データの周期性は捉えていません。

数式

数式予測は、データに周期性があり、量が上下する物理過程に従っている場合に使用できます。例えば、周囲温度は、1日および1年の周期性を示します。数式予測では、正弦曲線をフィットさせることができます。

数式予測は、量 y が支配方程式に従うと仮定します。

数学的な形式: y = f(t)

例:

• 指数数式

• 正弦数式

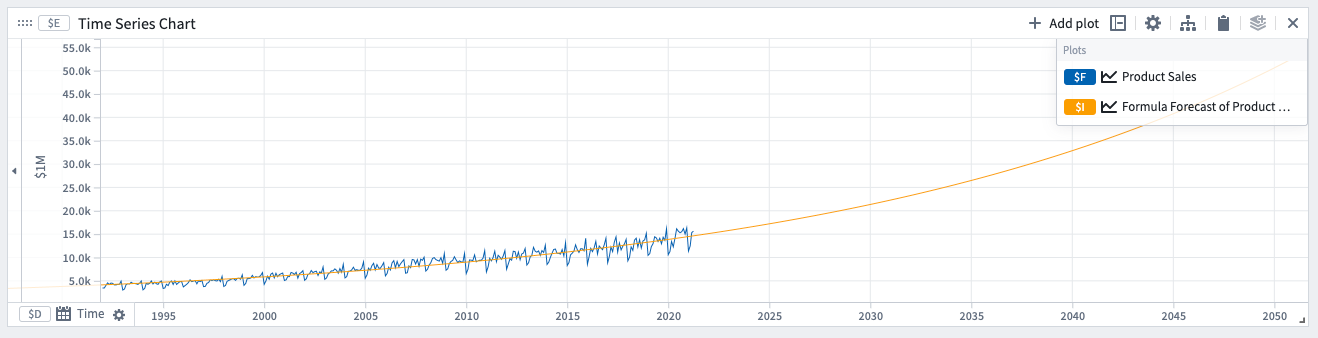
指数数式の例での予測。モデルによって決定された係数は、予測詳細の式に表示されます。

ODE (通常の微分方程式)

ODEは、通常の微分方程式によって支配される量を予測するために使用できます。ODE予測では、量 y の導関数（変化率）が支配方程式に従うと仮定します。

数学的な形式:

• 1次

  

• 2次

  

例:

• 指数成長（λ>0）または減衰（λ<0）

  

• ニュートンの第二法則（F=m*a）

  

• スプリングマスシステム、単純調和振動子

  

ODE予測を定義するには、未知数を @ プレフィックスと文字で定義した係数を使って、支配方程式を式ボックスに追加します。例えば、指数成長の場合、@k * y となります。ここで、y は量です。

この例では、指数成長方程式を使ったODE予測を使用しました。

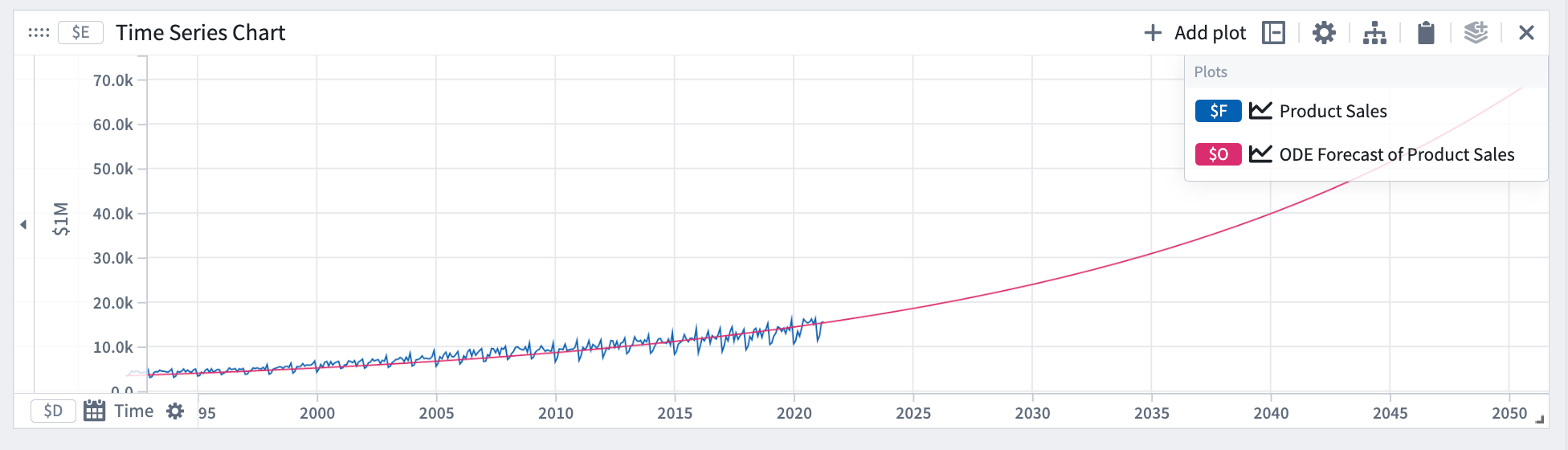
ARIMA (自己回帰統合移動平均)

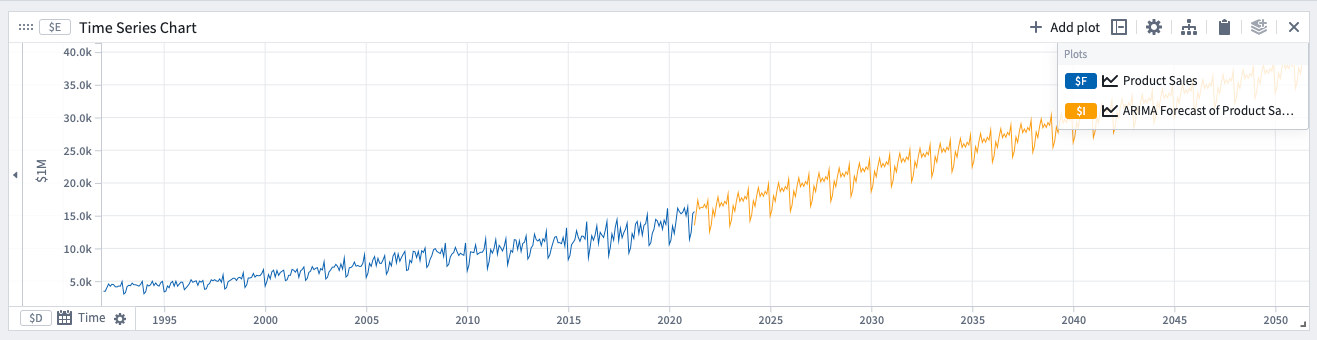
この予測は、データに周期性があり、生活のパターンから周期性が生じる場合に適しています。例えば、週に特定の曜日に買い物をする可能性が高い場合、小売りの売上に週次の周期性が生じます。

数学的な形式（非季節性）:

ここで: yd​ は、d 回の差分（連続した値を減算）を取った後の y です。

オプション

Auto

自動オプションを選択すると、次のARIMAパラメータが自動的に設定されます。好みでパラメータを手動で変更して、適切なフィットが得られるまで調整することもできます。ARIMAパラメータを手動で選択する場合は、より少ない項を持つシンプルなモデルがより一般化されるため、小さな数値を選択することをお勧めします。

ARIMAパラメータ:

• 自己回帰項の数（p）。
• 差分の回数（d）。
• 移動平均項の数（q）。

季節性

モデルに季節性成分を追加することができます。そのために、季節性のトグルを切り替えて、季節性の期間を指定します。例えば、週次の周期性がある日次データの場合は、7 を入力します。

自動オプションがオフの場合、次のパラメータが表示されます。

• 季節性自己回帰項の数（P）。
• 季節性差分の回数（D）。
• 季節性移動平均項の数（Q）。

さまざまな種類の損失

特定の予測タイプでは、フィッティング時に使用される損失の定義を選択できます。予測をトレーニングデータにフィットさせる際に、損失を最小化するように係数が選択されます。損失の種類によって、異なる予測が得られます。

二乗差の合計（デフォルト）

トレーニング時間範囲内の目標系列ポイント y[i] と予測 f[i] ポイント間の二乗差の合計の平方根。エラーの L2 ノルムに相当します。

絶対差の合計

トレーニング時間範囲内の目標系列ポイントと予測ポイント間の絶対差の合計。エラーの L1 ノルムに相当します。

最大絶対差

トレーニング時間範囲内の目標系列ポイントと予測ポイント間の最大絶対差。エラーの L-無限大（L∞）ノルムに相当します。