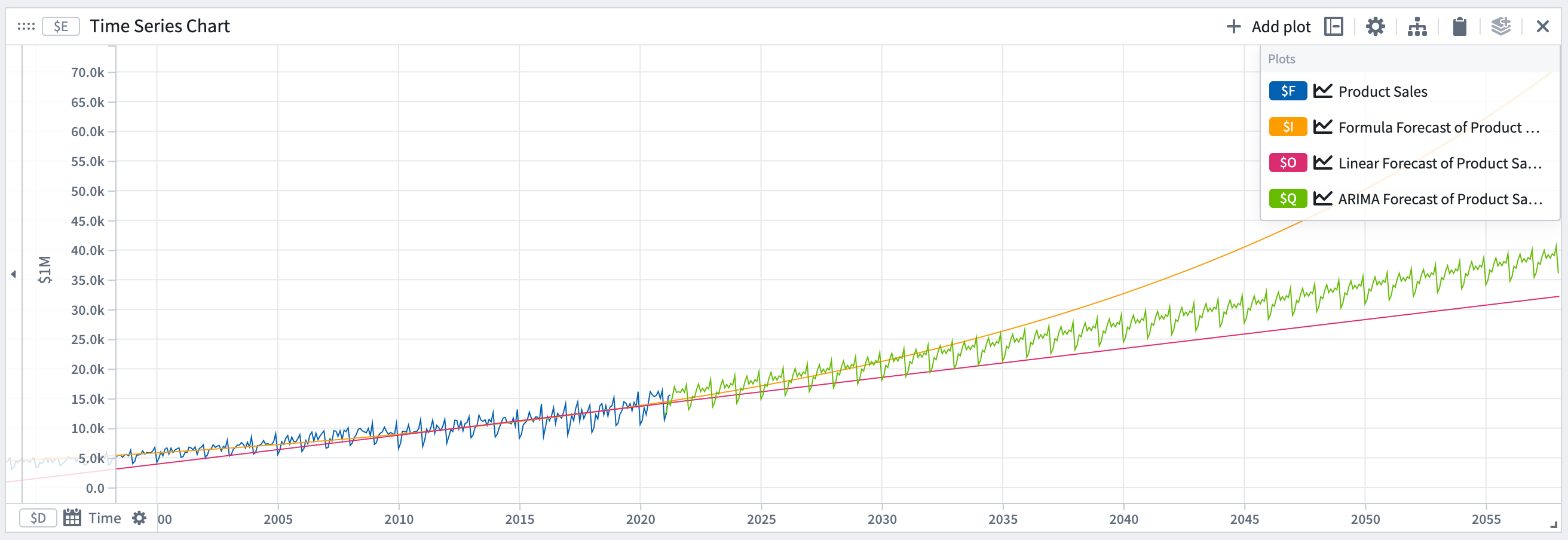
Forecast time series
You can create forecasts in Quiver using the Time series forecast transform. A forecast is a projection forward in time of an existing time series plot in your analysis. Forecasts in Quiver are built visually and interactively. The result of a forecast is a time series plot representing the forecasted data; this time series plot can be further transformed using Quiver’s time series transforms.
Input type
Time series
Output type
Time series
Usage information
| Functionality | Availability |
|---|---|
| Standard Quiver card | Supported |
| Transform table transform | Unsupported |
Create a forecast
To illustrate this section, we use the linear forecast as an example. Sections below give more details about each type of forecast.
- Add the time series you would like to forecast to your Quiver analysis by clicking Time Series from the analysis top bar to open the search bar. In our example, we want to forecast the sales of a product.
- Select Time Series Forecast from the Time Series menu.

- In the forecast editor, select the linear forecast type and then select the plot you added at step 1 as the input plot.

This will produce a time series plot (in this case, a line), that is by default fitted to the entire range of the input plot. Note that the time axis will remain the same as it was for the input time series plot. To see the forecast further into the future, you can zoom out on the x-axis.
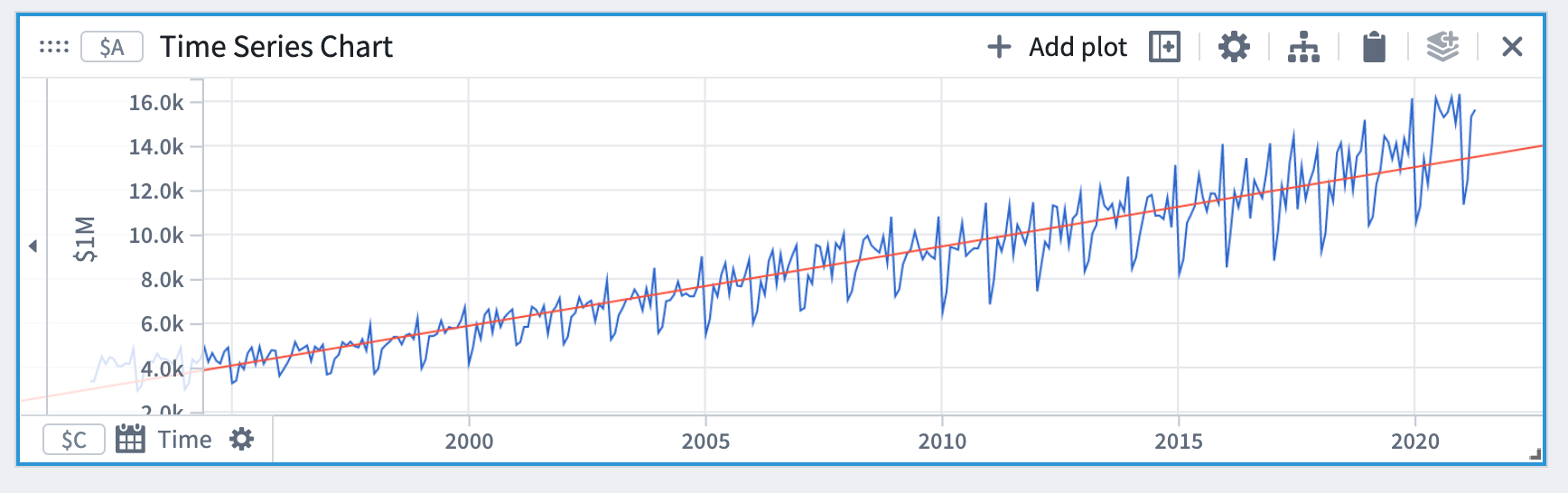
You can find the values of the coefficients under the Forecast Details section of the forecast editor.

In the linear forecast example, the coefficients are m (the slope) and c (the offset).
Optional steps
- To restrict the fitting to a particular time range, turn on the Use Training Time Range toggle and select a time range parameter.
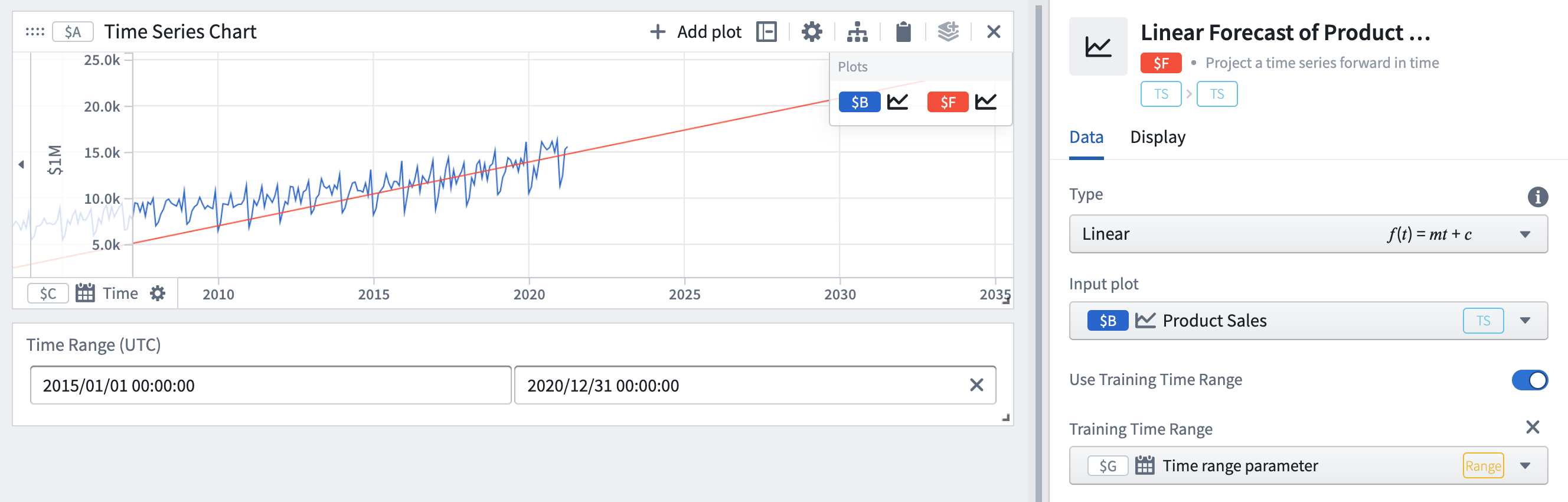
Here we have set the training time range to be 2015-2020 instead of the entire history. As a result, the parameters (slope and offset) of the forecast have changed to make the forecast more accurate for the training time range. This can be useful if you believe certain times will be more indicative of future behavior.
- Set coefficients boundaries. In the Coefficients section of the editor, switch on the toggles for the coefficients you want to set boundaries on. In this example, setting a boundary on the slope coefficient of this forecast changes both coefficients.

- Choose a loss definition. The default loss is the sum of squared differences, and the other options are the maximum absolute difference and the sum of absolute differences. When fitting the forecast to the training data, parameters will be selected to minimize the loss. Different types of loss will result in different forecasts. For more details refer to the losses section.

In our example, changing the loss definition results in different forecast coefficients.
The different types of forecasts
In this section, we detail the different types of forecast and their configuration options. For the remainder of the documentation, we refer to the quantity to be forecasted as y or y(t) to denote y at time t.
Constant
The constant forecast assumes the quantity y will remain constant.
Mathematical form: y = a
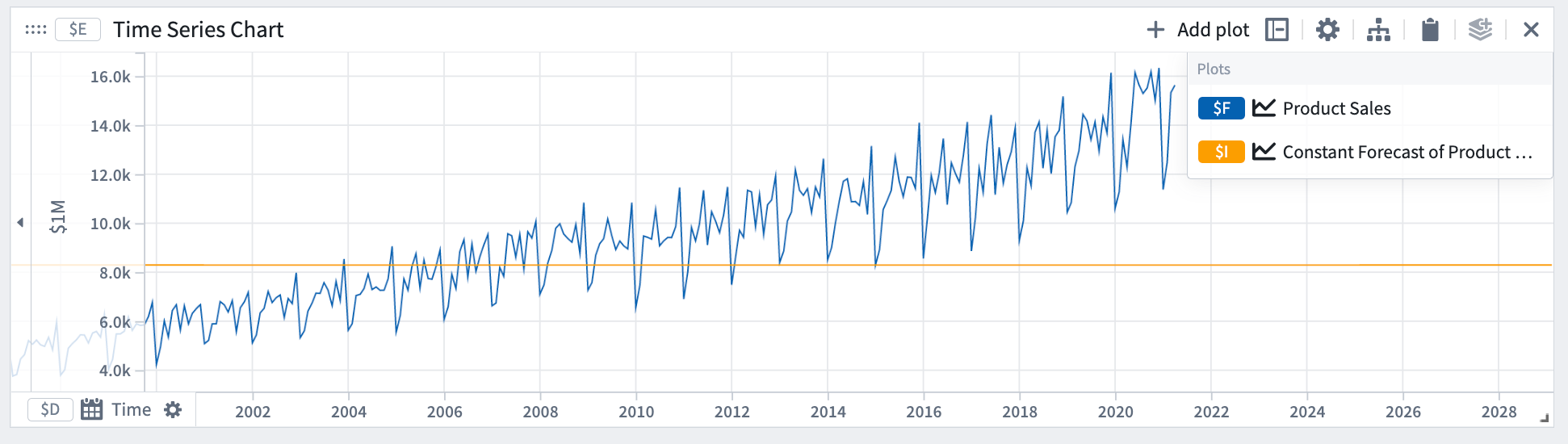
In our example, we can see that the constant forecast does not capture the slope or periodicity in the data.
Linear
The linear forecast assumes the quantity y will follow a linear trend.
Mathematical form: y = a*t + b
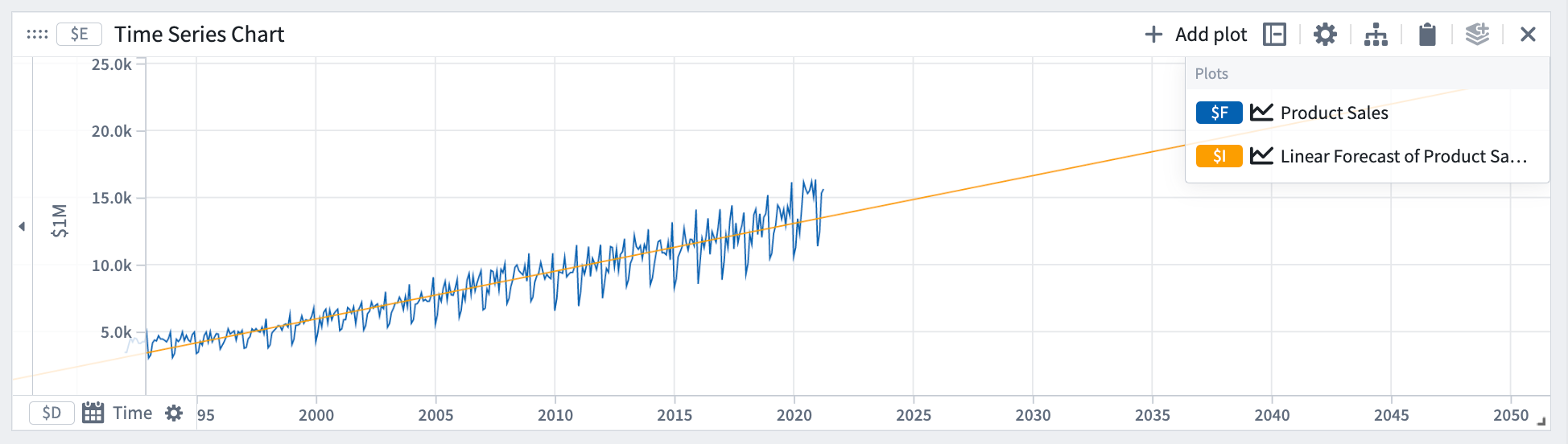
In our example, the linear forecast captures the slope but not the periodicity in the data.
Formula
Formula forecasts can be used when there is periodicity in the data, and the quantity is following some physical process that ebbs and flows. For example, ambient temperature exhibits both daily and yearly periodicity. The formula forecast allows you to fit a sinusoidal curve.
The formula forecast assumes the quantity y follows a governing equation.
Mathematical form: y = f(t)
Examples:
- Exponential formula

- Sinusoidal formula

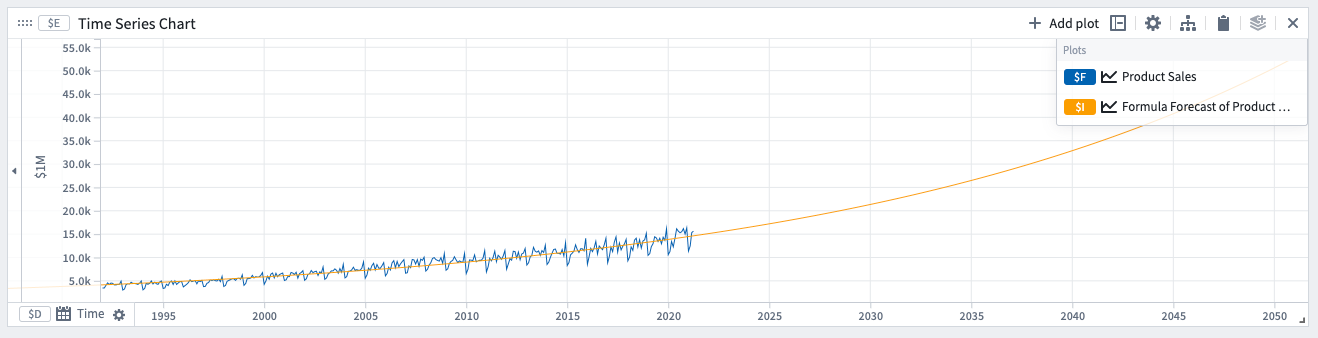
Example forecast with an exponential formula. The coefficients determined by the model are displayed in the expression under Forecast details.

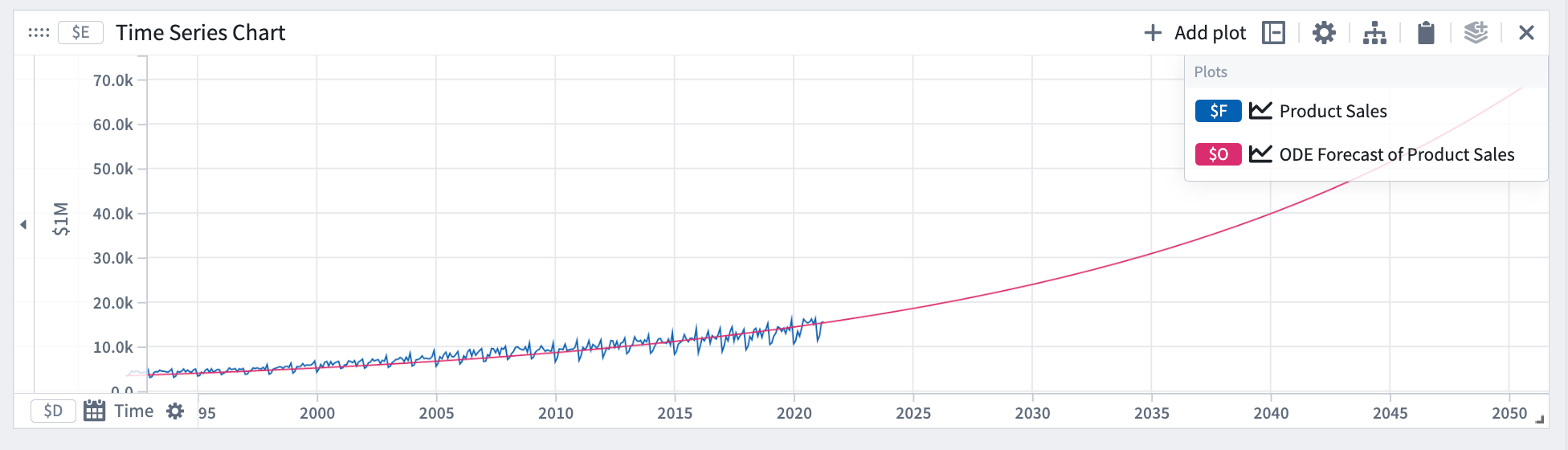
ODE (Ordinary differential equation)
ODE can be used to forecast a quantity that is governed by an Ordinary Differential Equation. The ODE forecast assumes the derivative (rate of change) of the quantity y follows a governing equation.
Mathematical form:
-
1st order

-
2nd order

Examples:
-
Exponential growth (λ>0) or decay (λ<0)

-
Newton's 2nd law (
F=m*a)
-
Spring mass system, simple harmonic oscillator

To define your ODE forecast, add the governing equation to the expression box with the unknowns defined as coefficients using the @ prefix and a letter. For example, for exponential growth we have @k * y, where y is the quantity.

In this example, we used an ODE forecast using the exponential growth equation.
ARIMA (Autoregressive integrated moving average)
This forecast is indicated when there is periodicity in the data coming from some pattern of life. For example, retail sales exhibit some weekly periodicity if people are more likely to shop on certain days of the week.
Mathematical form (non-seasonal):

Where:
yd is y after differences (subtract consecutive values) have been taken d times.
Options
Auto
Selecting the auto option will set the following ARIMA parameters for you automatically. If you prefer, you can change the parameters manually until you get a satisfactory fit. If selecting the ARIMA parameters manually, bias toward smaller numbers as a simpler model with less terms will generalize better.
ARIMA parameters:
- Number of autoregressive terms (p).
- Number of differences taken (d).
- Number of moving average terms (q).
Seasonal
It is possible to add a seasonal component to the model. To do so, switch the seasonal toggle and specify the period of seasonality. For example, if you have daily data with weekly periodicity, enter 7.
If the auto option is off, the following parameters will appear:
- Number of seasonal autoregressive terms (P).
- Number of seasonal differences taken (D).
- Number of seasonal moving average terms (Q).
The different types of losses
For certain forecast types, you can choose the loss definition used when fitting the forecast. When fitting the forecast to the training data, the coefficients will be selected to minimize the loss. Different types of loss will result in different forecasts.
Sum of squared differences (default)
The square root of the sum of square differences between the target series points y[i] and the forecast f[i] points within the training time range. Equivalent to the L2 norm of the error.

Sum of absolute differences
The sum of absolute differences between the target series points and the forecast points within the training time range. Equivalent to the L1 norm of the error.

Maximum absolute difference
The maximum absolute difference between the target series points and the forecast points within the training time range. Equivalent to the L-infinity (L∞) norm of the error.
