- Capabilities
- Getting started
- Architecture center
- Platform updates
Window functions
The PostgreSQL documentation ↗ defines window functions as follows:
A window function performs a calculation across a set of table rows that are somehow related to the current row. This is comparable to the type of calculation that can be done with an aggregate function. But unlike regular aggregate functions, use of a window function does not cause rows to become grouped into a single output row — the rows retain their separate identities. Behind the scenes, the window function is able to access more than just the current row of the query result.
This documentation explains the syntax of some window functions you might want to use in Contour expressions. For more background information on window functions, see the following additional resources:
- Window Functions (PostgreSQL documentation) ↗
- SQL Window Function (Mode Analytics tutorial) ↗
- SQL Window Functions Introduction (Apache Drill) ↗
- Analytic Functions (Oracle documentation) ↗
Basic syntax
At its most basic, a window function can be broken down into:
<function> OVER <some window>
where the function is one of the supported aggregate functions and the window is a subset of rows in the table.
You can omit the window by using () – this applies the function to all rows in the table.
The following example will add an entry to every row with the maximum value in the date column.
MAX("date") OVER ()
PARTITION BY
You can also add an optional PARTITION BY clause before the window definition. PARTITION BYgroups rows within the window based on the values in a given column. The aggregate function is then applied to each partition separately.
For example, in a table with person records, the following expression calculates the total number of males and females, and adds a count to each row for the gender value in that row:
COUNT("person_id") OVER (PARTITION BY "gender")
ORDER BY
For expressions where you do define the window, you must specify the bounds of the window as well as how to sort the rows in the table. This sub-expression can be simplified to:
<how to sort table> ROWS BETWEEN <start location> AND <end location>
where “how to sort table” is (1) which column to sort by and (2) whether to sort ascending or descending.
There are the following possibilities for specifying the bounds of the window (“start location” and “end location”):
UNBOUNDED PRECEDING: From the start of the table to the current row.n PRECEDING(e.g.2 PRECEDING): From n rows before the current row to the current row.CURRENT ROWn FOLLOWING(e.g.5 FOLLOWING): From the current row to n rows after the current row.UNBOUNDED FOLLOWING: From the current row to the end of the table.
Here is an example table with each of the above possibilities labeled:
FIRST_NAME |
------------
Adam |<-- UNBOUNDED PRECEDING
... |
Alison |
Amanda |
Jack |
Jasmine |
Jonathan | <-- 1 PRECEDING
Leonard | <-- CURRENT ROW
Mary | <-- 1 FOLLOWING
Tracey |
... |
Zoe | <-- UNBOUNDED FOLLOWING
(Source: blog.jooq.org ↗)
So, given a table with sales records, you could use the following to find the average value of a sale over the last 5 sales:
AVG("sale_value") OVER (ORDER BY "date_of_sale" ASC
ROWS BETWEEN 4 PRECEDING AND CURRENT ROW)
“The last 5 sales” is the window. The sub-expression after OVER sorts the table by date, then for each row, calculates the average across the 4 preceding rows and the current row.
Putting it all together
The following complex example brings together all of the syntax mentioned above. This expression shows the cumulative number of sales, grouped by product category, up to the current sale.
COUNT("sale_id") OVER (PARTITION BY "product_category"
ORDER BY "date_of_sale" ASC
ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW)
Note that entries are now sorted by partition – in other words, the table is partitioned first, and then rows are sorted within each partition.
More examples
Say you have a table recording items you have purchased. You could use the following window function to derive a new column for a running total of purchases:
SUM("item_cost") OVER (ORDER BY "purchase_date" ASC
RANGE BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW )
To calculate the running total grouped by category, you can add partitions:
SUM(“item_cost”) OVER (PARTITION BY “category”
ORDER BY “purchase_date” ASC
RANGE BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW)
This would partition the rows by the “category” column, sort the rows within each category by purchase date, and calculate the running total for the cost of all items in that category.
Examples with meteorites data
You can try out the following examples yourself with the meteorite landings dataset. This dataset comes from The Meteoritical Society via the NASA Data Portal ↗.
This expression calculates the largest meteorite in each class:
MAX("mass") OVER (PARTITION BY "class" )
If we derive a new column max_size_by_class with the above window function:
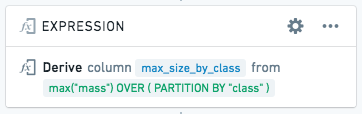
… then the resulting table will look like this:
| name | class | mass | max_size_by_class |
|---|---|---|---|
| Jiddat al Harasis 450 | H3.7-5 | 217.741 | 3879 |
| Ramlat as Sahmah 422 | H3.7-5 | 3879 | 3879 |
| … | |||
| Beni Semguine | H5-an | 18 | 33.9 |
| Miller Range 07273 | H5-an | 33.9 | 33.9 |
| … | |||
| Allan Hills 88102 | Howardite | 8.33 | 40000 |
| Allan Hills 88135 | Howardite | 4.75 | 40000 |
| … | |||
| Yamato 81020 | CO3.0 | 270.34 | 3912 |
| Northwest Africa 2918 | CO3.0 | 237 | 3912 |
To calculate the cumulative sum (running total) of mass by meteorite class over time:
Copied!1 2 3 4SUM("mass") OVER (PARTITION BY "class" ORDER BY "year" ASC ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW )
This partitions the table by meteorite class, sorts each partition by date, and then for each row, calculates the sum of the current row plus all previous rows in the mass column, and adds that sum as a new column in the current row.
To calculate the total (not running) sum of mass by meteorite class:
Copied!1SUM("mass") OVER (PARTITION BY "class")
This aggregation might not be useful by itself, but if we expand it, we can calculate a more interesting statistic – what percentage does this meteorite contribute to the total mass for the class?
Copied!1"mass" / (SUM("mass") OVER (PARTITION BY "class")) * 100
To calculate the total number (count) of meteorites found for each class:
Copied!1COUNT("id") OVER (PARTITION BY "class")
Non-determinism
When using ROW_NUMBER, FIRST, LAST, ARRAY_AGG, or ARRAY_AGG_DISTINCT, in a window function, be careful of nondeterminism. Imagine we are partitioning by column A and ordering by column B. If for the same value of column A, there are multiple rows with the same value of column B, the results of these window functions may be non-deterministic -- they may produce different results given the same input data and logic.