시계열 예측

Quiver에서 시계열 예측 변환을 사용하여 예측을 생성할 수 있습니다. 예측은 분석에서 기존 시계열 플롯의 시간을 앞으로 확장하는 것입니다. Quiver의 예측은 시각적이고 상호 작용적으로 구축됩니다. 예측의 결과는 예측된 데이터를 나타내는 시계열 플롯이며, 이 시계열 플롯은 Quiver의 시계열 변환을 사용하여 추가로 변환할 수 있습니다.

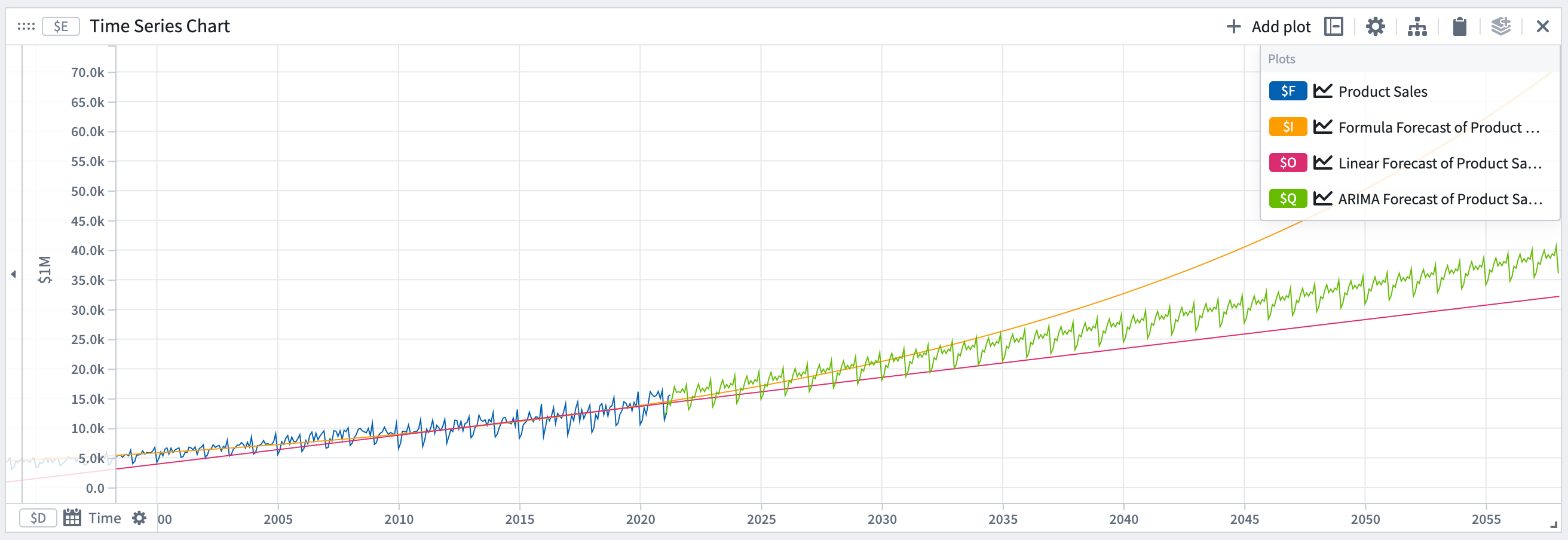
예측 생성

이 섹션을 설명하기 위해 선형 예측을 예로 들겠습니다. 아래 섹션에서 각 예측 유형에 대한 자세한 내용을 제공합니다.

1. 예측하려는 시계열을 Quiver 분석에 추가하려면 분석 상단 표시줄에서 시계열을 클릭하여 검색 창을 여십시오. 예시로, 제품의 판매량을 예측하려고 합니다.

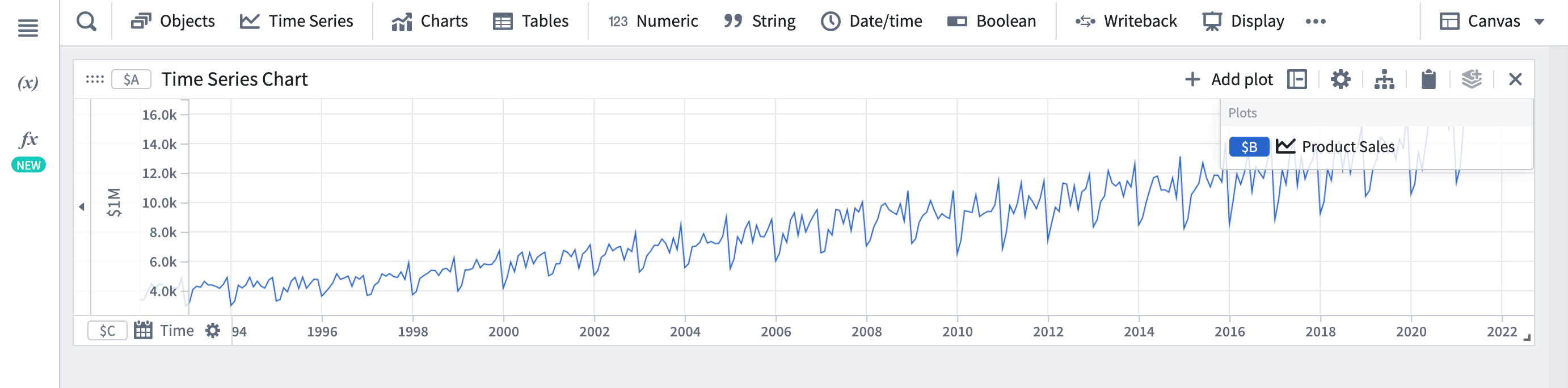
2. 시계열 메뉴에서 시계열 예측을 선택합니다.

3. 예측 에디터에서 선형 예측 유형을 선택한 다음 입력 플롯으로 1단계에서 추가한 플롯을 선택합니다.

이렇게 하면 입력 플롯의 전체 범위에 기본적으로 맞춰진 시계열 플롯(이 경우 선)이 생성됩니다. 시간 축은 입력 시계열 플롯의 경우와 동일하게 유지됩니다. 미래의 예측을 더 보려면 x축에서 확대/축소할 수 있습니다.

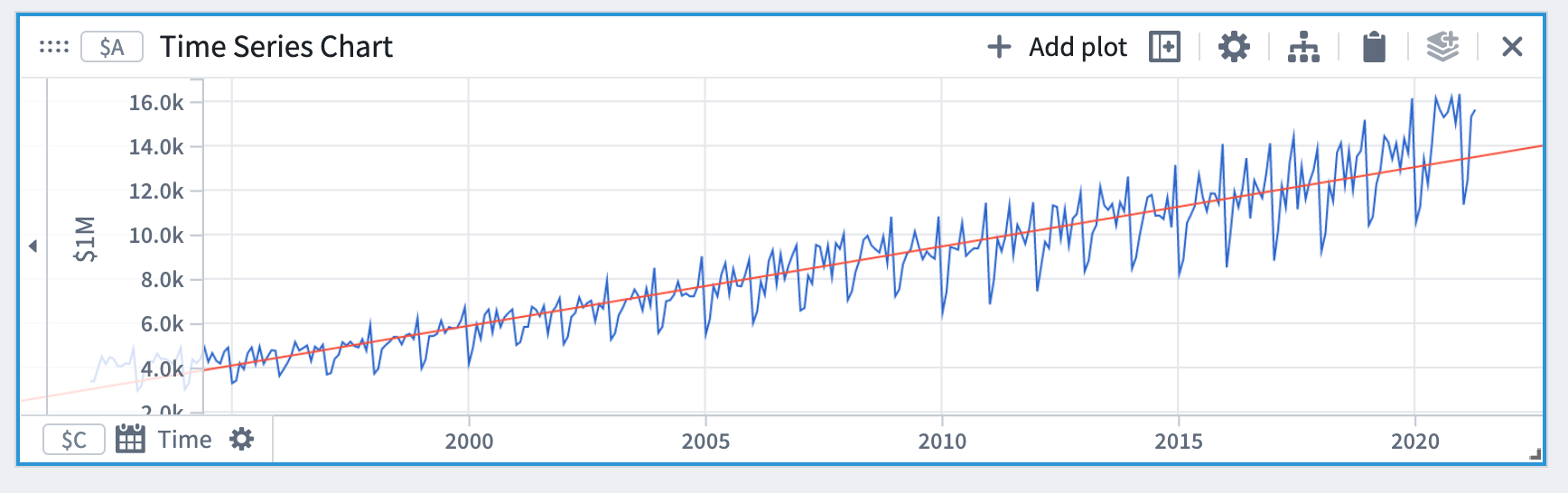
계수 값은 예측 에디터의 예측 상세 섹션에서 확인할 수 있습니다.

선형 예측의 경우 계수는 m (기울기)와 c (오프셋)입니다.

선택적 단계

1. 특정 시간 범위에 맞추려면 훈련 시간 범위 사용 토글을 켜고 시간 범위 파라미터를 선택합니다.

여기에서 훈련 시간 범위를 전체 기록 대신 2015-2020으로 설정했습니다. 결과적으로 예측의 파라미터(기울기와 오프셋)가 변경되어 훈련 시간 범위에 대한 예측이 더 정확해집니다. 특정 시간이 미래 행동을 더 잘 나타낼 것으로 생각되는 경우 유용할 수 있습니다.

2. 계수 경계 설정. 에디터의 계수 섹션에서 경계를 설정하려는 계수에 대한 토글을 켭니다. 예시로, 이 예측의 기울기 계수에 경계를 설정하면 두 계수가 모두 변경됩니다.

3. 손실 정의 선택. 기본 손실은 제곱 차이의 합이며, 다른 옵션은 최대 절대 차이와 절대 차이의 합입니다. 훈련 데이터에 예측을 맞추는 동안, 손실을 최소화하는 파라미터가 선택됩니다. 손실의 다른 유형은 다른 예측을 생성할 것입니다. 자세한 내용은 손실 섹션을 참조하십시오.

예시에서 손실 정의를 변경하면 예측 계수가 달라집니다.

다양한 예측 유형

이 섹션에서는 다양한 예측 유형과 그 구성 옵션에 대해 설명합니다. 문서의 나머지 부분에서 예측할 양을 y 또는 시간 t에서의 y를 나타내기 위해 y(t)로 참조합니다.

상수

상수 예측은 양 y가 일정하게 유지될 것이라고 가정합니다.

수학적 형태: y = a

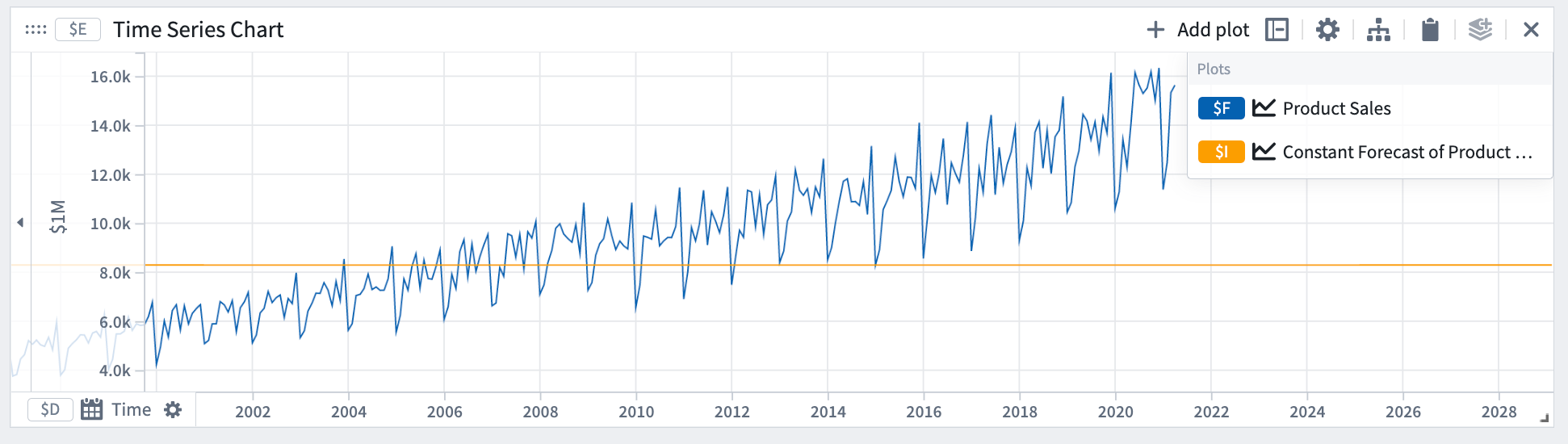
예시에서 상수 예측은 데이터의 기울기나 주기성을 포착하지 못했습니다.

선형

선형 예측은 양 y가 선형 추세를 따를 것이라고 가정합니다.

수학적 형태: y = a*t + b

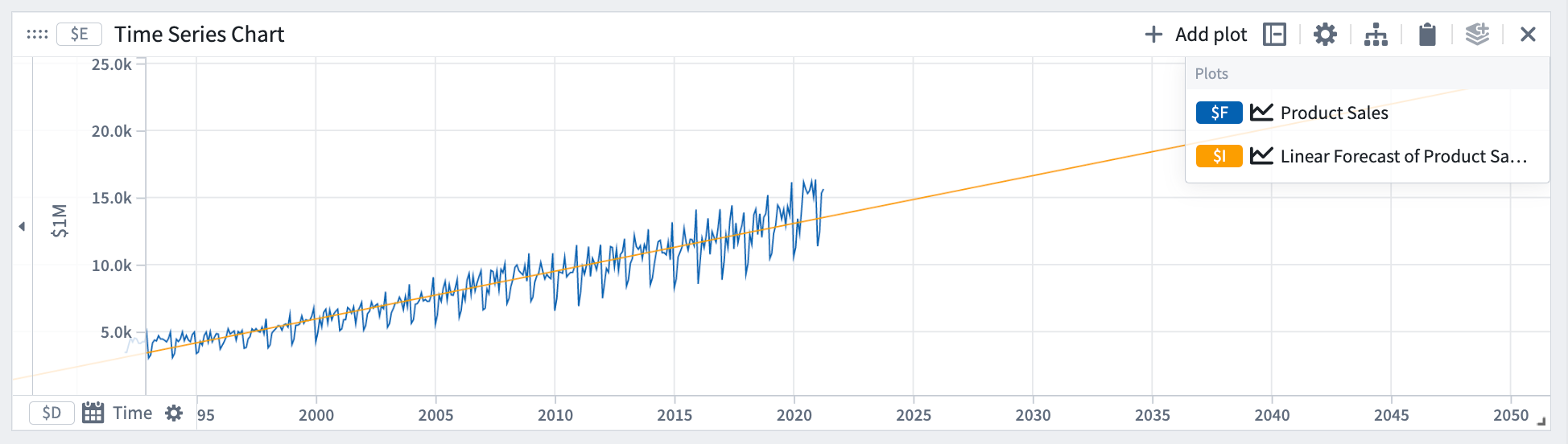
예시에서 선형 예측은 데이터의 기울기는 포착하지만 주기성은 포착하지 못했습니다.

공식

데이터에 주기성이 있고 일부 물리적 과정에 따라 양이 상승하고 하강하는 경우 공식 예측을 사용할 수 있습니다. 예를 들어, 주변 온도는 하루와 일년 주기성을 모두 나타냅니다. 공식 예측을 사용하면 사인 곡선을 맞출 수 있습니다.

공식 예측은 양 y가 지배 방정식을 따른다고 가정합니다.

수학적 형태: y = f(t)

예시:

• 지수 공식

• 사인 공식

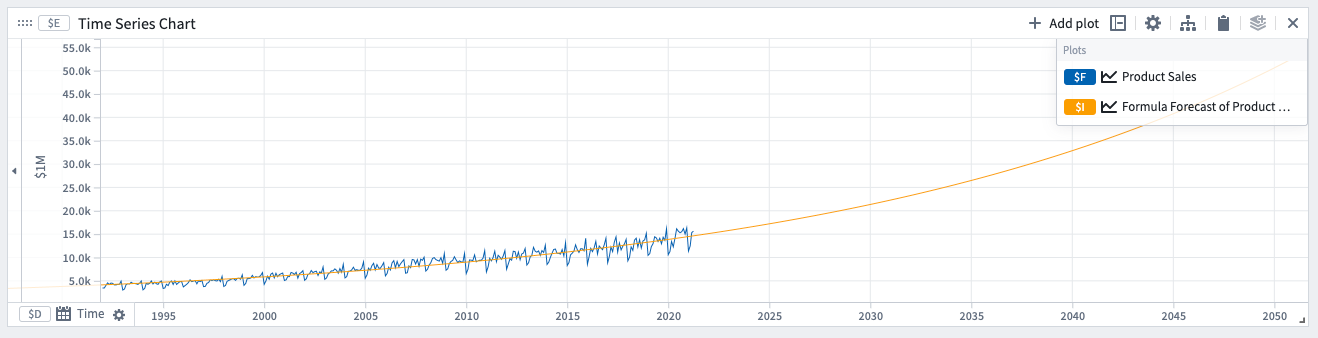
지수 공식을 사용한 예측 예시입니다. 모델에서 결정한 계수는 예측 상세 아래 표현식에서 표시됩니다.

ODE (일반 미분 방정식)

ODE는 일반 미분 방정식에 의해 조절되는 양을 예측하는 데 사용할 수 있습니다. ODE 예측은 양 y의 미분(변화율)이 지배 방정식을 따른다고 가정합니다.

수학적 형태:

• 1차

  

• 2차

  

예시:

• 지수 성장 (λ>0) 또는 감소 (λ<0)

  

• 뉴턴의 제2법칙 (F=m*a)

  

• 스프링 질량 시스템, 단순 조화 진동자

  

ODE 예측을 정의하려면 알 수 없는 계수를 @ 접두사와 문자를 사용하여 지배 방정식을 표현 상자에 추가합니다. 예를 들어, 지수 성장의 경우 @k * y를 사용하며, 여기서 y는 양입니다.

이 예시에서는 지수 성장 방정식을 사용한 ODE 예측을 사용했습니다.

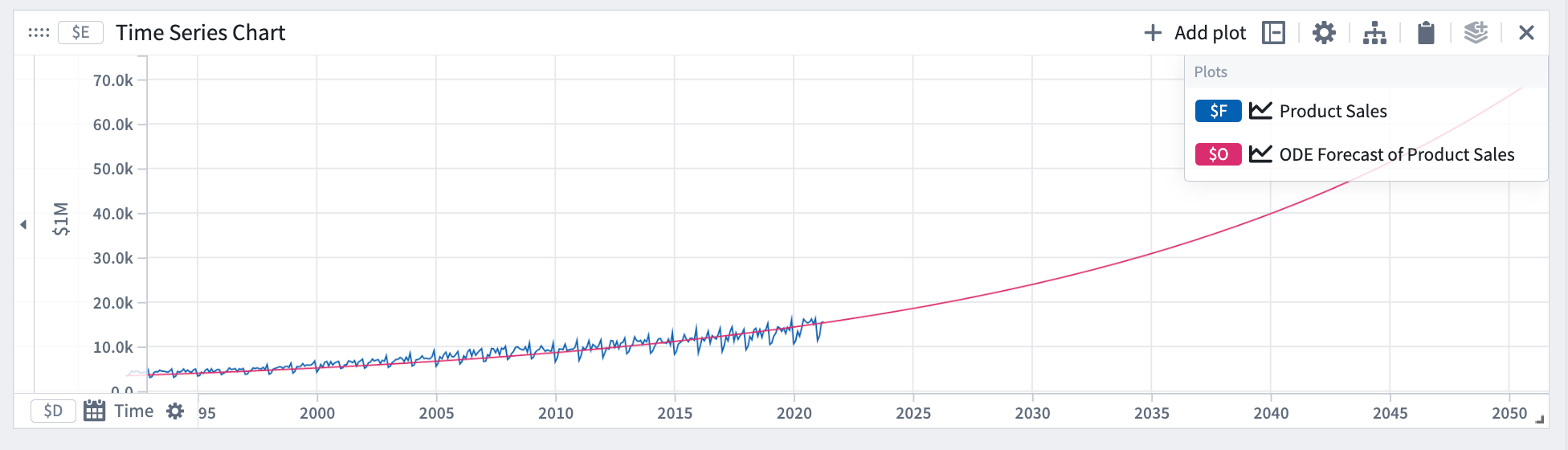
ARIMA (자기회귀누적이동평균)

이 예측은 일생의 어떤 패턴으로 인해 데이터에 주기성이 있는 경우 적합합니다. 예를 들어, 사람들이 주중 특정 날에 더 자주 쇼핑하는 경우 소매 판매량에 주간 주기성이 나타납니다.

수학적 형태 (비계절적):

여기서: yd​는 차이(연속 값 빼기)를 d번 취한 후의 y입니다.

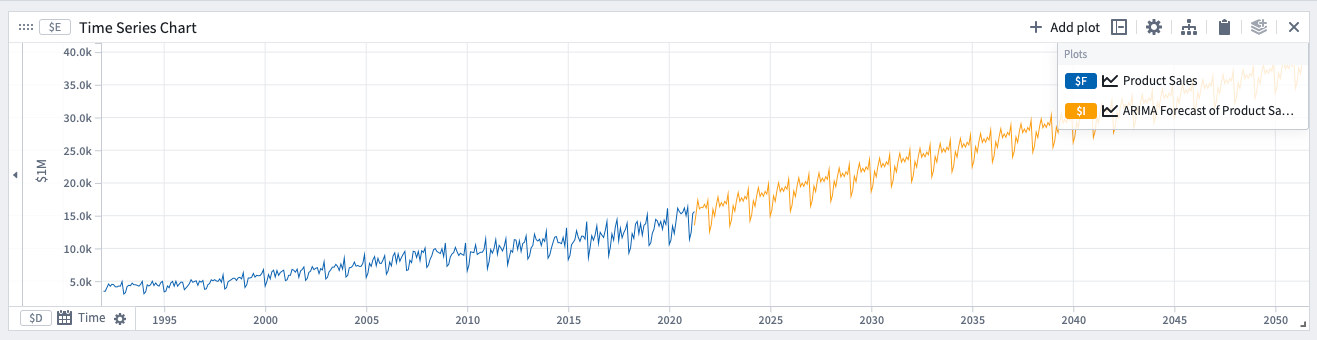
옵션

자동

자동 옵션을 선택하면 다음 ARIMA 파라미터가 자동으로 설정됩니다. 원하는 경우 파라미터를 수동으로 변경하여 만족스러운 적합성을 얻을 수 있습니다. ARIMA 파라미터를 수동으로 선택하는 경우, 더 간단한 모델로 더 나은 일반화를 할 수 있는 더 작은 수치로 편향하십시오.

ARIMA 파라미터:

• 자기회귀 항의 수 (p).
• 차분 횟수 (d).
• 이동 평균 항의 수 (q).

계절

모델에 계절성 성분을 추가할 수 있습니다. 그렇게 하려면 계절 토글을 전환하고 계절성 기간을 지정합니다. 예를 들어, 주기성이 있는 일일 데이터가 있는 경우 7을 입력합니다.

자동 옵션이 꺼져 있는 경우 다음 파라미터가 나타납니다:

• 계절 자기회귀 항의 수 (P).
• 계절 차분 횟수 (D).
• 계절 이동 평균 항의 수 (Q).

다양한 손실 유형

특정 예측 유형의 경우 예측을 맞추는 데 사용되는 손실 정의를 선택할 수 있습니다. 예측을 훈련 데이터에 맞추는 동안 손실이 최소화되도록 계수가 선택됩니다. 다양한 손실 유형은 다른 예측을 생성할 것입니다.

제곱 차이의 합 (기본)

목표 시리즈 점 y[i]와 예측 f[i] 점 사이의 제곱 차이의 합의 제곱근은 훈련 시간 범위 내에서 계산됩니다. 오류의 L2​ 노름과 동일합니다.

절대 차이의 합

목표 시리즈 점과 예측 점 사이의 절대 차이의 합은 훈련 시간 범위 내에서 계산됩니다. 오류의 L1​ 노름과 동일합니다.

최대 절대 차이

목표 시리즈 점과 예측 점 사이의 최대 절대 차이는 훈련 시간 범위 내에서 계산됩니다. 오류의 L-무한대 (L∞​) 노름과 동일합니다.